
How Useful is Feature Visualization?
Welcome back! This post marks Part 3 in our ongoing series on neural understanding, where we work through a practical example with some representative techniques in order to understand what and how a neural network has learned.
While Part 2 walked through a sample problem, this post contains a collection of results to analyze! Quite a bit of results, in fact. So, maybe take some time out to stretch and do some calisthenics while following along.
As always, the Jupyter notebooks may be found here.
What is Feature Visualization?
In the old days of Machine Learning (ML) a feature was an attribute of an example. For example, when trying to classify a sample data set concerning cancer biopsies, features might be the average width of the cells in the sample, the average perimeter of the cells, and the opacity of the cells. A feature describes an object that the ML algorithm is trying to reason about. In numerical datasets, a feature represents a column of data. In visual datasets, a feature is a collection of pixels, perhaps the edge of an object or the texture of part of the object.
In pre-deep learning times, some sort of feature engineering took place before feeding a dataset to an ML algorithm. In visual domains, this included things like detecting all the edges in an image or finding all the “blobs”. In the era of Deep Learning, part of the job of the neural network is to find these features themselves (or at least that is the theory). Unfortunately, due to the black box nature of neural networks, it is not obviously clear that this actually happens.
Feature visualization is the umbrella term for creating an image to suggest what a given neuron or group of neurons have learned. Google has done a great deal of work on feature visualization recently, with DeepDream being perhaps the most famous.

This example comes from Google’s inception network that was trained to identify roughly 20,000 different objects, many of them different breeds of dogs. This feature visualization is from one of the neurons in a deep layer of the network. Notice that it looks remarkably like a dog’s ear, furthermore, a specific type of dog ear. What this is saying is that when attempting to identify a species of dog in an image, the network is using the shape of the ear to make a determination. This is clear evidence of how the network operates!

Upon examining the visualizations of their lower-level layers, viewers can see that they start with simple line detectors and then move up to more complicated textures. This is exactly in line with the theory of deep learning.
How Does It Work?
The basic version of feature visualization asks, for a given neuron, what input image results in the highest activation? This is known as HappyMap. Basically, what sort of input to the network makes this neuron the most active or “happy”? Google has also experimented with the inverse, SadMaps. Here’s the basic gist:
- Select a neuron.
- Create a random image. In this type of image, each pixel takes on a random value independent of nearby pixels. The result looks very much like TV static.
- Feed the image to the network and observe the output of the selected neuron.
- Adjust the image so that the output of the neuron is greater than the observed amount.
- Repeat steps 3 to 5 until the output of the neuron cannot be increased.
- Output the adjusted image as the HappyMap.
In practice, this is accomplished by performing a gradient descent search on the input space, keeping the weights constant. Unfortunately, this process alone doesn’t usually result in interpretable HappyMaps. As each pixel is adjusted independently of its neighbors, the result can still be somewhat noisy and hard to interpret. So, usually, a normalizing function is added to the optimization. The normalizing function penalizes an image for not being “natural enough”. This can be required that the pixels conform to some standard or that neighborhoods of pixels do not look too different.
What We Did
Google makes their experiments on inception freely available in collab notebooks that ship with Lucid, the software behind the experiments. They also provide scattered instructions on how to replicate these experiments by using a tensorflow trained network. However, we use Keras here, and though Keras does run on top of tensorflow, there was no way to save a Keras model such that the Google collab notebooks would work. Even following the instructions didn’t work!
In the end, we did find a wonderful tool, keras-vis — that allows the same types of visualizations that Lucid allows, but works out of the box on Keras.
The notebooks built can be found in experiments/experiment1 and various subdirectories.
A few notes are in order. First of all, keras-vis uses two regularizers or normalizers. The first is basically an old fashioned p norm. The idea here is to minimize the values that the input pixels can take. This keeps the values from going crazy, beyond the range of allowable RGB values. The second norm is the total variation norm. Total variation norm tries to minimize the variation in a group of pixels. This one turned out to be crucially important for getting good visuals. Keras-vis allows the user to weight the main activation maximization function with the two normalizing functions. In practice, we experimented with various levels of total variation, from 1e-5 to 1e3. It was observed that good visuals tended to occur for filters at 1e-3 or 1e-2 and 1e1 for dense neurons. Our experiments did not find any significant effect of changing the norm weight.
Secondly, the input to this process is a random image. Any optimization process that starts from a random input is not guaranteed to end up with the same outputs. Put simply, each time you generate a HappyMap from a given neuron, it is likely to be different than any previous attempts. The hope, and our experience, is that the maps do tend to look similar (you will need to watch out for random noise). In several cases, a HappyMap showed an interesting pattern that was not seen to generate again across multiple attempts –so be careful before drawing conclusions.
Initial Results
Take a look at experiments/experiment1/visualization_first_pass.ipynb. At the top of the notebook you can find some code for loading the model and functions for wrapping the keras-vis visualize_activation function. After seeing the results that Google achieved on their visualization results and the results displayed on the keras-vis documentation, we were excited to see what our output neurons would show. Multiple weight levels were tested and displayed the different results in the notebook.

It’s clear that our results are not nearly as straightforward or, well, exciting. Neuron 0 (labeled as filter 0) is the one that codes for “not facing left”. Neuron 1 (labeled as filter 1) codes for “facing left”. The HappyMap for neuron 1, does sort of look like a face pointing to camera left (if you squint). One interesting thing to note is that the HappyMap for not facing left appears to be the complement of the facing left neuron. In a softmax layer, the sum of all the activations must be one. Since in the two class problem there are only two neurons, whatever maximizes the activation of one neuron naturally minimizes the other neuron.
This begs the question: Would this get better results without using a softmax layer? Or using a multi class problem?
Continuing on in the notebook, the first three convolution layers were visualized. Some of the layers were visualized many times with different weights for the total visualization norm. Looking at conv2d_1, the first convolution layer, there are some interesting results.
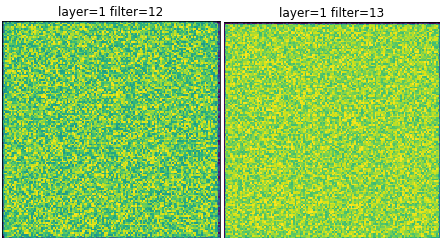
The first is that some neurons, when viewed with different weights always seem to produce a pattern that appears to be random noise. These appear to be neurons that don’t have a pattern, nothing makes them particularly happy. So they are likely not used deeper into the network. This signals that there may be more convolution filters than necessary.
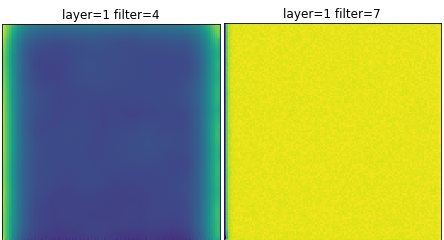
There are also some neurons that under various weights appear to be most happy when the input is bright. Are these ambient light detectors? Or are they neurons that simply like anything? Is this more evidence for having excess convolution filters?
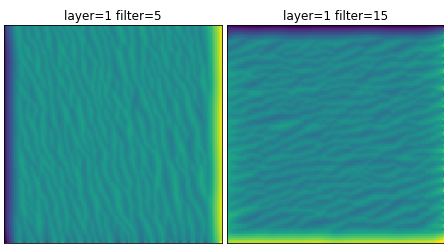
The rest of the neurons in that layer exhibit the same characteristics that were seen in the Google examples. There are wavy lines that appear to be the edge detectors that Google talked about.
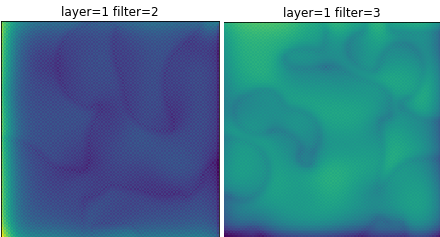
There are also quite a few neurons, about half, for which no discernable pattern forms. At some weights, these neurons present a blue background with graceful curves. It’s tempting to think that these might be some sort of curve operator? But running the results multiple times didn’t yield any consistent patterns. So the question arises again: Are there more filters than necessary?
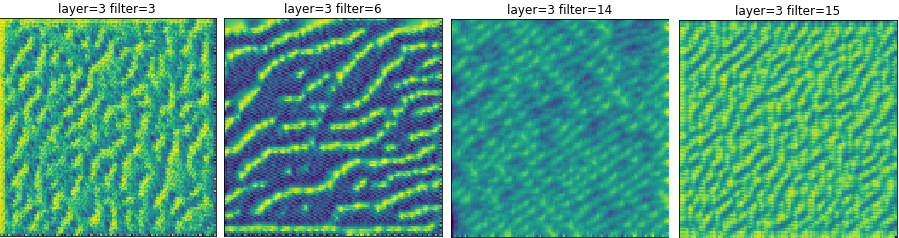
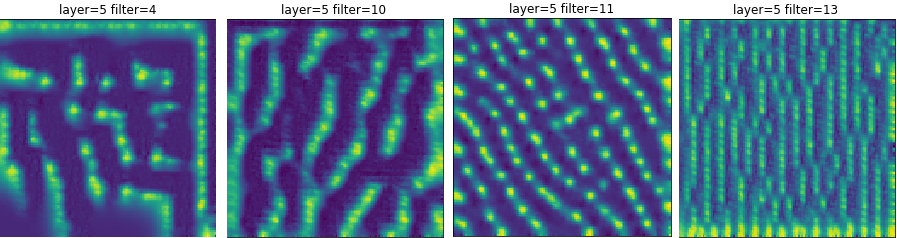
conv2_2 and conv2_3 show some pretty interesting results. The neurons seem to be activated by more complicated patterns than just lines. Often, there is a two dimensional structure, as if these layers are looking for corners and angles. In fact, almost every neuron in this layer yields a recognizable pattern. Additionally, many of the neurons have HappyMaps that seem to code for edges of various thickness as well. It seems as if something about the texture of an image is being learned.

Now turn to experiments/experiment1/visualization_dense_layers.ipynb. This notebook shows the results of running on the dense layers. Each of the neurons in these layers responds well to visualization in that a pattern is evident. What seems to be happening is that there are neurons that respond to events in certain locations. Could these be the object or part of object detectors that we were promised? If so, they must encode for something entirely different because they’re much unlike Google’s neurons. Are they looking for ears? Noses? Something in the environment? There certainly isn’t a dog or floppy ear detector like Google’s. Hmmm….
WHAT’S NEXT?
Why are our results so different? Do we not have enough layers? Do we not have enough wide enough layers? Or, do we have too many dense neurons? Answering these questions will need some additional finesse. To address each individual point, we’ll have to run some quick follow-ups and see what happens. But that’s a debacle for another day. Join us next time as we run some test experiments!







